This lecture introduced EM algorithm: an iterative technique to estimate probaility models for missing data. Meanwhile, mixture Gaussian, PCA and factor analysis are actually *generative* models in a way of EM.

Key points

• EM: An iterative technique to estimate probability models for data with missing components or information
  • By iteratively “completing” the data and reestimating parameters
• PCA: Is actually a generative model for Gaussian data
  • Data lie close to a linear manifold, with orthogonal noise
  • A lienar autoencoder!
• Factor Analysis: Also a generative model for Gaussian data
  • Data lie close to a linear manifold
  • Like PCA, but without directional constraints on the noise (not necessarily orthogonal)

Generative models

Learning a generative model

• You are given some set of observed data $X=\{x\}$
• You choose a model $P(x ; \theta)$ for the distribution of $x$
  • $\theta$ are the parameters of the model
• Estimate the theta such that $P(x ; \theta)$ best “fits” the observations $X=\{x\}$
• How to define "best fits"?
  • Maximum likelihood!
  • Assumption: The data you have observed are very typical of the process

EM algorithm

• Tackle missing data and information problem in model estimation
• Let $o$ are observed data

$\log P(o)=\log \sum_{h} P(h, o)=\log \sum_{h} Q(h) \frac{P(h, o)}{Q(h)}$

• The logarithm is a concave function, therefore

$\log \sum_{h} Q(h) \frac{P(h, o)}{Q(h)} \geq \sum_{h} Q(h) \log \frac{P(h, o)}{Q(h)}$

• Choose a tight lower bound

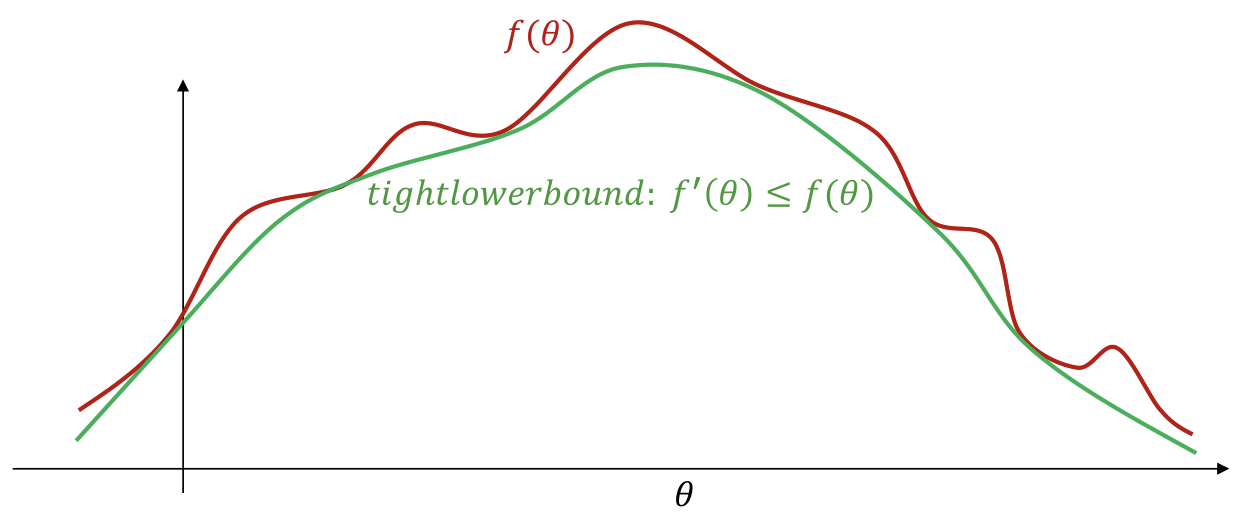
• Let $Q(h)=P(h \mid o ; \theta^{\prime})$

$\begin{aligned} \log P(o ; \theta) \geq \sum_{h} P\left(h \mid o ; \theta^{\prime}\right) \log \frac{P(h, o ; \theta)}{P\left(h \mid o ; \theta^{\prime}\right)} \end{aligned}$

• Let $J\left(\theta, \theta^{\prime}\right)=\sum_{h} P\left(h \mid o ; \theta^{\prime}\right) \log \frac{P(h, o ; \theta)}{P\left(h \mid o ; \theta^{\prime}\right)}$

$\begin{array}{l} \log P(o ; \theta) \geq J\left(\theta, \theta^{\prime}\right) \end{array}$

• The algorithm process

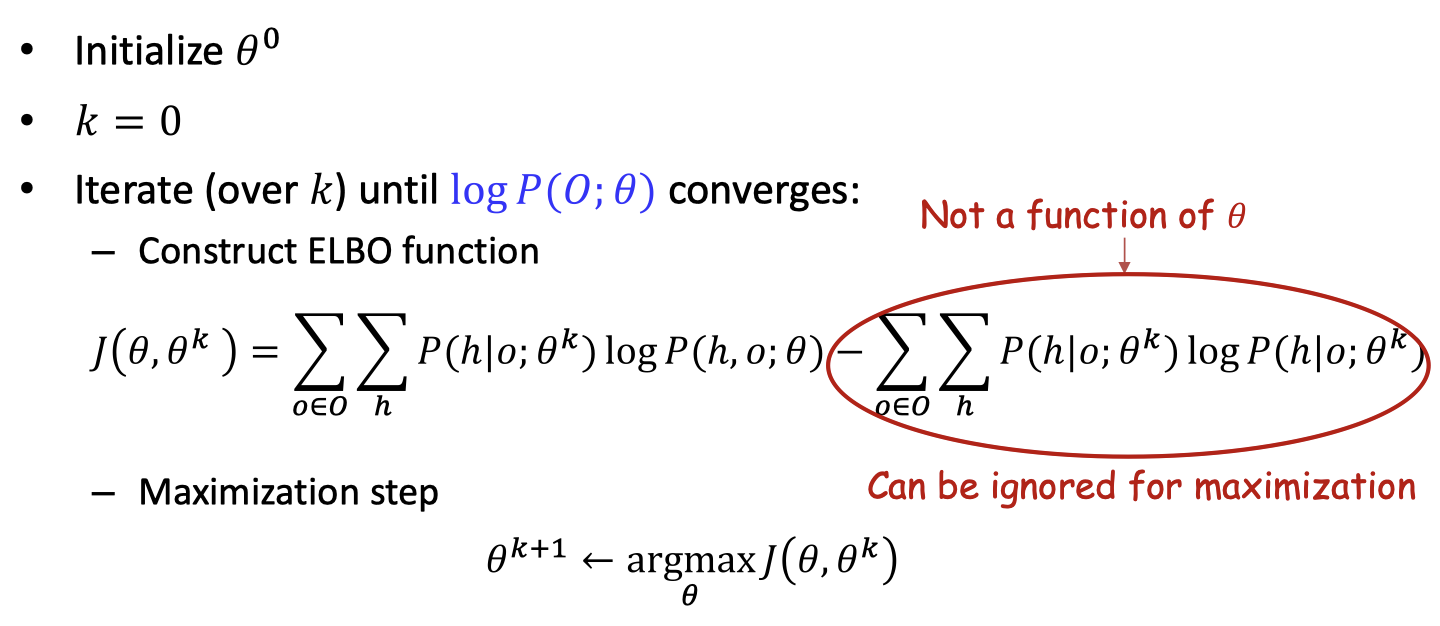
EM for missing data

• “Expand” every incomplete vector out into all possibilities
  • With proportion $P(m|o)$ (from previous estimate of the model)
• Estimate the statistics from the expanded data

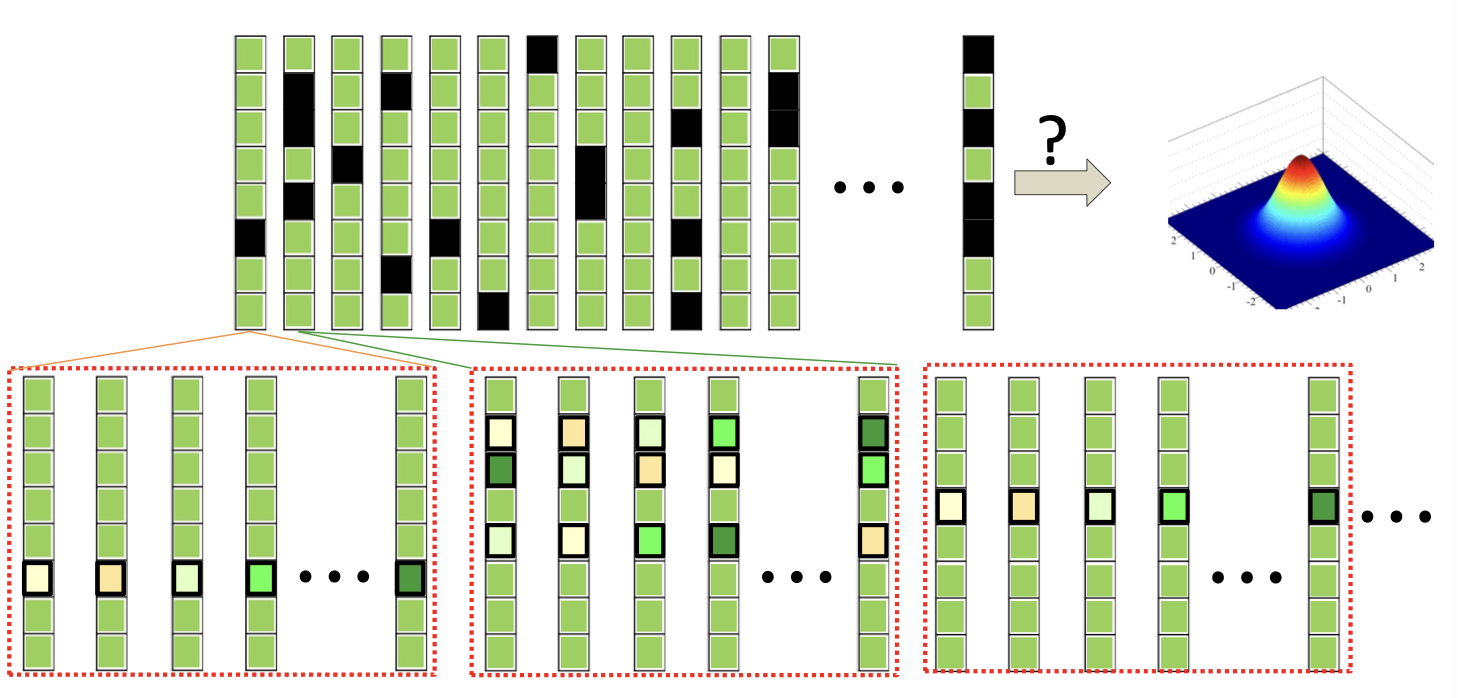
EM for missing information

• Problem : We are not given the actual Gaussian for each observation
  • What we want: $\left(o_{1}, k_{1}\right),\left(o_{2}, k_{2}\right),\left(o_{3}, k_{3}\right) \ldots$
  • What we have: $o_{1}, o_{2}, o_{3} \ldots$

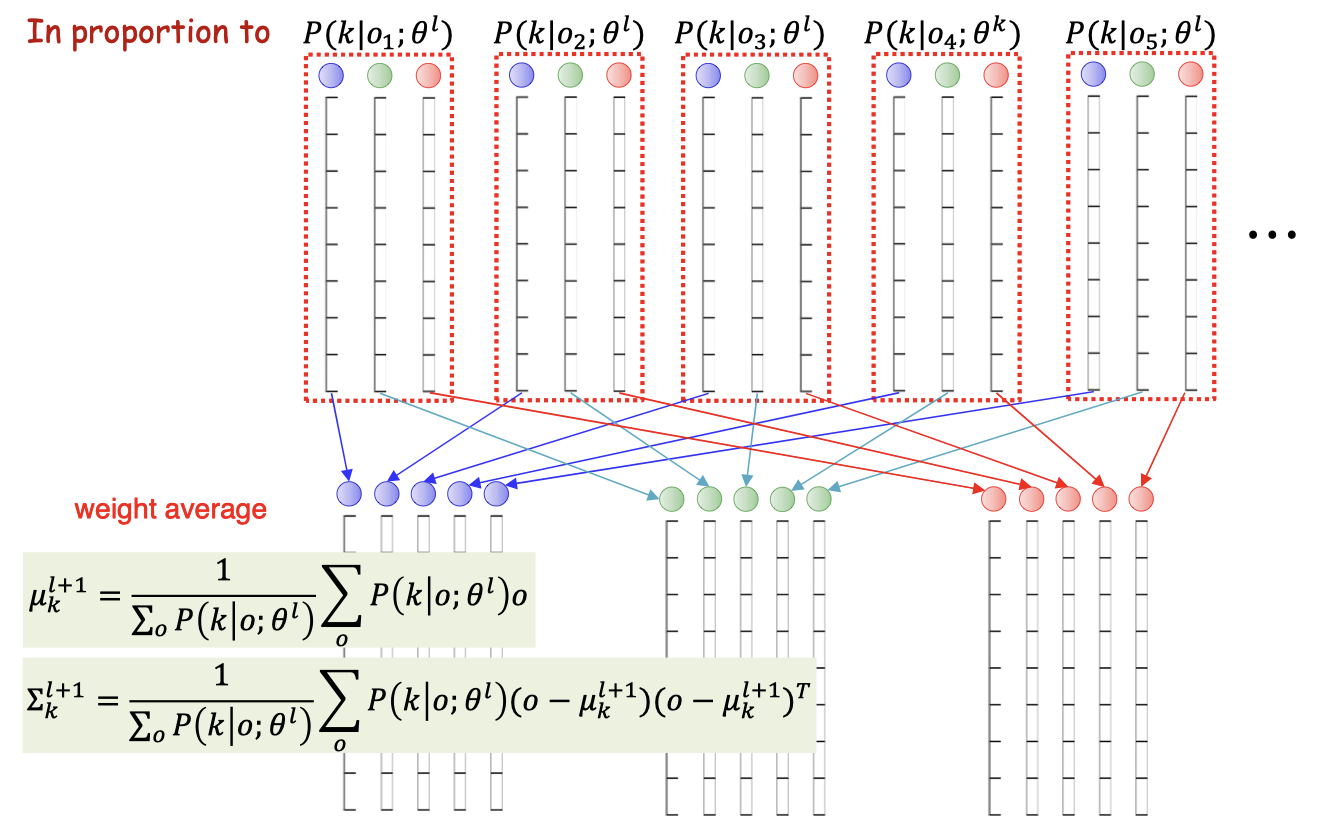
• The algorithm process

General EM principle

• “Complete” the data by considering every possible value for missing data/variables
• Reestimate parameters from the “completed” data

Principal Component Analysis

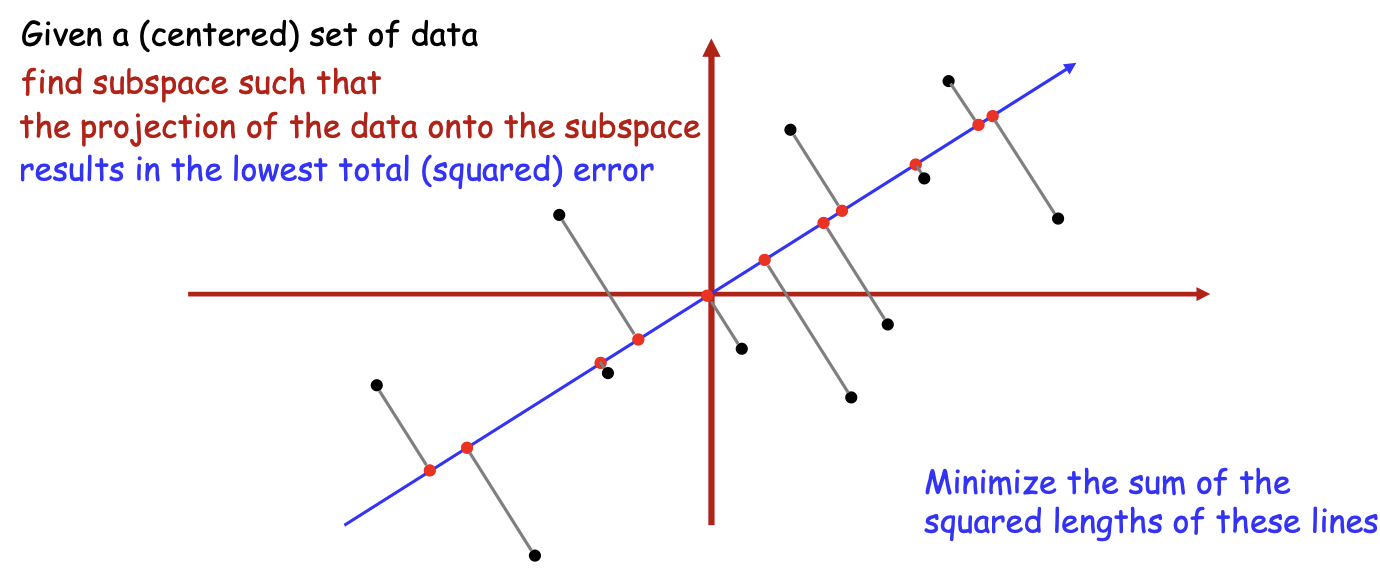
• Find the principal subspace such that when all vectors are approximated as lying on that subspace, the approximation error is minimal

Closed form

• Total projection error for all data

$L=\sum_{x} x^{T} x-w^{T} x x^{T} w$

• Minimizing this w.r.t 𝑤 (subject to 𝑤 = unit vector) gives you the Eigenvalue equation

$\left(\sum_{x} x^{T} x\right) w=\lambda w$

• This can be solved to find the principal subspace
  • However, it is not feasible for large matrix (need to find eigenvalue)

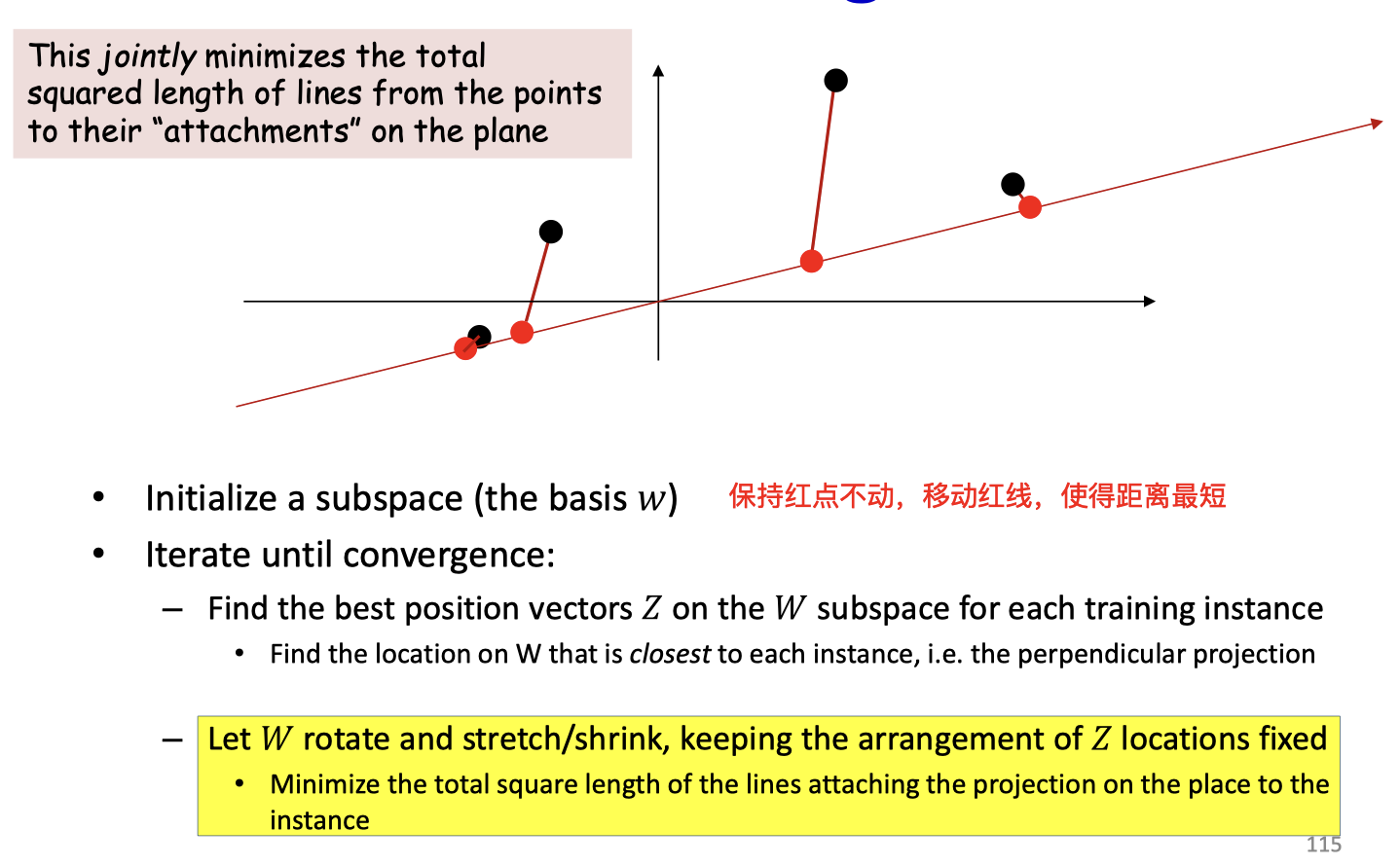
Iterative solution

• Objective: Find a vector (subspace) $w$ and a position $z$ on $w$ such that $zw\approx x$ most closely (in an L2 sense) for the entire (training) data

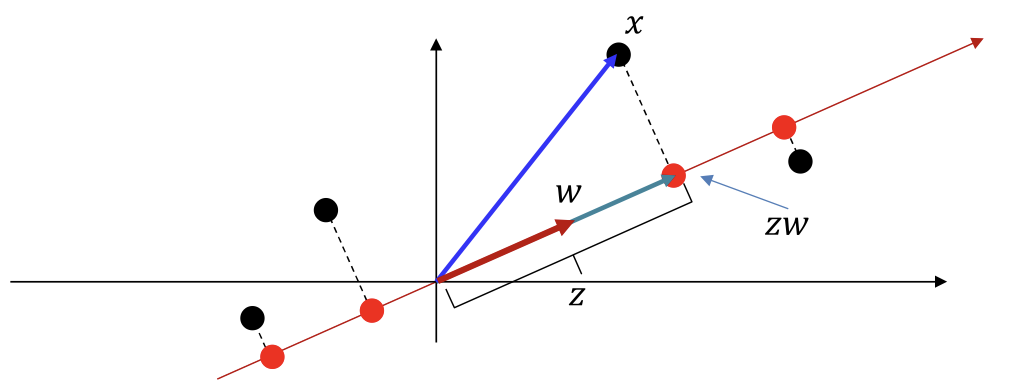
• The algorithm process

PCA & linear autoencoder

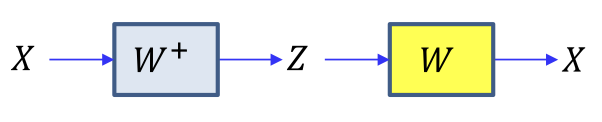
• We put data $X$ into the inital subpace, got $Z$
• The fix $Z$ to get a better subpace $W$, etc...
• This is an autoencoder with linear activations !
  • Backprop actually works by simultaneously updating (implicitly) and in tiny increments
• PCA is actually a generative model
  • The observed data are Gaussian
  • Gaussian data lying very close to a principal subspace
  • Comprising “clean” Gaussian data on the subspace plus orthogonal noise